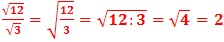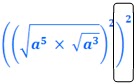Potenciação
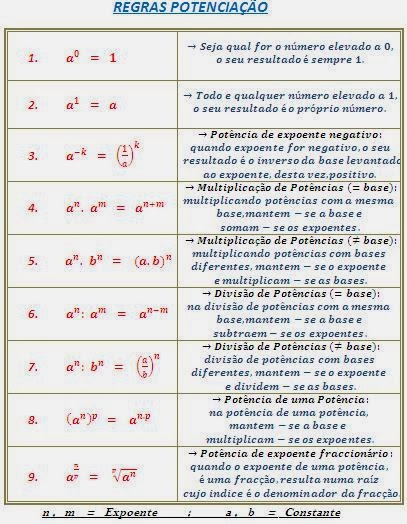 |
| Regras Potenciação (Potencias). |
 |
| Radical, Radicando, Índice |
Quando o índice da raiz, n, é omitido; então é assumido como índice daquela raiz o valor2. Ou seja n = 2.
Conforme se espera; toda a raiz deve ter um resultado real x, onde a correspondência entre estes é expressa abaixo.
 |
| Regras Radiciação (Raizes). |
Definições e Demonstrações:
Raiz de 1 quociente e quociente de 2 raizes: o quociente de 2 radicais do mesmo indice, é o radical do mesmo indice cujo o radicando é quociente dos radicandos do divisor e do dividendo.
Raiz de 1 Raiz: A raiz de indice n da raiz de indice p de um certo numero e a raiz de indicen.p desse numero.
Raiz de 1 produto e produto de 1 raiz: A raiz de um produto e igual ao produto das raizes do mesmo indice.
Multiplicação de Potencia da mesma base (no caso base -3): O produto de potencia da mesma base é a potencia com a mesma base cujo expoente é a soma dos expoentes dos factores.
Divisão de potencias com a mesma base (base -2): O quociente de potencias com a mesma base é uma potencia com a mesma base e cujo o expoente é a diferença entre os expoentes do dividendo e do divisor.
Potencia de expoente fraccionário: Reciprocamente todo o radical é convertivel em potencia de expoente fraccionário.
Potencia de uma potencia: A potencia de uma potencia éoutra potência com a base da 1ª e expoente igual ao produto dos expoentes.
Inversamente/o: Qualquer coefiente ou factor de um radical pode passar pode passar para factor do seu radicando desde que se multiplique o seu expoente pelo indice do radical.
Os Exercicios seguintes 1., 2. e 3. são os mais importantes para a manipulação fluente de potencias e raizes, verifique com atenção a simplicidade das operações:
O proximo exercicio vem demonstrar o porquê das operaçoes entre coeficientes (o nº fora da raiz) e radicando (o nº dentro da raiz) são possiveis.
Quando o indice da raiz for igual ao expoente do radicando, o radicando com expoente = ao indice da raiz passa a coeficiente dessa mesma raiz.
Exercícios:
Vamos resolver alguns exercicios simples da utilização de potencia e radicais, saliento, a simplicidade destes exercicios farão com que domine muito bem esse tipo de operações podendo posteriormente tentar resolver exercicios maiores e mais complexos.
1. Efectue as divisões e multiplicações propostas:
NOTA: Existe diferença entre o uso dos sinais:
 : significa equivalente; usa-se quando não é feito cálculo nehum mas sim um arranjo, simplificação, moldagem do exercicio de forma a que possamos percebe-lo melhor.
: significa equivalente; usa-se quando não é feito cálculo nehum mas sim um arranjo, simplificação, moldagem do exercicio de forma a que possamos percebe-lo melhor.
2. Efectue os seguintes cálculos elevando ao quadrado cada um dos exercícios propostos:
No exercicio seguinte, Não se preocupe com a utilização de letras, só precisa assumir a letra como se fosse um numero qualquer do qual nao sabe o valor.

Resolucão 2.2
1. O exercicio 2., propoe que se eleve ao quadro, assim colocamos tudo entre parenteses indicando que se vai englobar todo o calculo no quadrado:
2. Segundo a regra Potencia de uma Potencia multiplicam-se os dois expoentes de potencia:
3. Conforme a regra Inversamento qualquer coeficiente pode passar para radicando (para dentro da raiz) desde que se multiplique o seu expoente pelo expoente da raiz:
4. Seguinte, a regra Multiplicação de potencia da mesma base diz que se as base forem iguais entao da-se uma a mesma base e somam-se os seus expoentes:
3. Calcule utilizando as operações de potências :
Raiz de 1 produto e produto de 1 raiz: A raiz de um produto e igual ao produto das raizes do mesmo indice.
Multiplicação de Potencia da mesma base (no caso base -3): O produto de potencia da mesma base é a potencia com a mesma base cujo expoente é a soma dos expoentes dos factores.
Divisão de potencias com a mesma base (base -2): O quociente de potencias com a mesma base é uma potencia com a mesma base e cujo o expoente é a diferença entre os expoentes do dividendo e do divisor.
Potencia de expoente fraccionário: Reciprocamente todo o radical é convertivel em potencia de expoente fraccionário.
Potencia de uma potencia: A potencia de uma potencia éoutra potência com a base da 1ª e expoente igual ao produto dos expoentes.
Inversamente/o: Qualquer coefiente ou factor de um radical pode passar pode passar para factor do seu radicando desde que se multiplique o seu expoente pelo indice do radical.
Os Exercicios seguintes 1., 2. e 3. são os mais importantes para a manipulação fluente de potencias e raizes, verifique com atenção a simplicidade das operações:
O proximo exercicio vem demonstrar o porquê das operaçoes entre coeficientes (o nº fora da raiz) e radicando (o nº dentro da raiz) são possiveis.
Quando o indice da raiz for igual ao expoente do radicando, o radicando com expoente = ao indice da raiz passa a coeficiente dessa mesma raiz.
Exercícios:
Vamos resolver alguns exercicios simples da utilização de potencia e radicais, saliento, a simplicidade destes exercicios farão com que domine muito bem esse tipo de operações podendo posteriormente tentar resolver exercicios maiores e mais complexos.
1. Efectue as divisões e multiplicações propostas:
NOTA: Existe diferença entre o uso dos sinais:
 : significa equivalente; usa-se quando não é feito cálculo nehum mas sim um arranjo, simplificação, moldagem do exercicio de forma a que possamos percebe-lo melhor.
: significa equivalente; usa-se quando não é feito cálculo nehum mas sim um arranjo, simplificação, moldagem do exercicio de forma a que possamos percebe-lo melhor.
: o sinal de igual; apresenta sempre um resultado é sempre realizada alguma operação (soma, divisão, subtracção ou multiplicação).
2. Efectue os seguintes cálculos elevando ao quadrado cada um dos exercícios propostos:
No exercicio seguinte, Não se preocupe com a utilização de letras, só precisa assumir a letra como se fosse um numero qualquer do qual nao sabe o valor.

Resolucão 2.2
1. O exercicio 2., propoe que se eleve ao quadro, assim colocamos tudo entre parenteses indicando que se vai englobar todo o calculo no quadrado:
2. Segundo a regra Potencia de uma Potencia multiplicam-se os dois expoentes de potencia:
3. Conforme a regra Inversamento qualquer coeficiente pode passar para radicando (para dentro da raiz) desde que se multiplique o seu expoente pelo expoente da raiz:
5. Continuando, aplica-se a regra Raiz de uma raiz onde tem-se 2 raizes com o mesmo indice ou expoente, 2, multiplicam-se entao os seus expoentes e como seu produto resulta numa só raiz:
3. Calcule utilizando as operações de potências :